Sei g v e ein ungerichteter graph ohne schlingen. G heißt kreisfrei wenn es in g von jedem knoten u zu jedem anderen knoten v höchstens einen weg gibt.
Einfacher Graph Wikipedia
Eine folge v 0 v 1.
Einfacher weg graph. Ein graph der einen weg mit den knoten b c f sowie die kantenfolge d d e e e b b b a a a e e e f f enthält in der graphentheorie bezeichnet weg pfad kantenzug oder kantenfolge eine folge von knoten in welcher jeweils zwei aufeinanderfolgende knoten durch eine kante verbunden sind. Wpdatatables is a popular wordpress table plugin used to quickly create tables table charts from excel csv php and other data sources. Es sei g v e ein graph.
N heißt kantenzug. V n von knoten mit e i vi 1 v i e für i 1 2. Use our wp table plugin to represent vast amounts of complicated data in concise user friendly way using tables or charts.
Ein einfacher graph auch schlichter graph ist in der graphentheorie ein ungerichteter graph ohne mehrfachkanten und ohne schleifen. Ein einfacher weg p v w heißt m alternierend wenn die kanten abwechselnd zu m und nicht zu m gehören. Falls zusätzlich gilt dass die endknoten m exponiert sind dann heißt p m augmentierend.
Die länge des weges ist n. Ein einfacher graph ist also ein geordnetes paar v e displaystyle v e wobei v displaystyle v eine endliche menge von knoten und e displaystyle e eine menge von kanten ist. Die knoten vj paarweise verschieden sind.
Ein weg heißt einfacher weg gdw. G heißt zusammenhängend wenn es in g von jedem knoten u zu jedem anderen knoten v mindestens einen weg gibt. Ein kantenzug bei dem die kanten ei alle verschieden sind heißt weg.
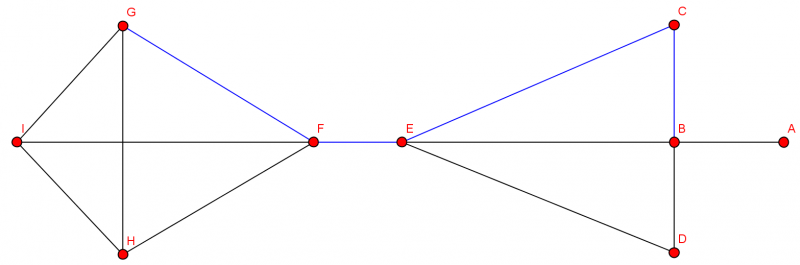Grundbegriffe Der Graphentheorie 1 Programmingwiki
Ingwer Wasser Wirkt Entzundungshemmend Und Kurbelt Die Fettverbrennung An Food Foodlover Foodlover Foodfacts Foodfact Fett Bauch Weg Effektiv Abnehmen
Weg Graphentheorie Wikipedia
Toms Schnelle Mathe Helfer Bestimmte Integrale Berechnen Touchdownmathe Tomsschnellemathehelfer Bestimmteintegrale Integrale Integ Knowledge Study School
0 Comments